埃尔德什致密乌拉姆:他是神童,亦然神叟
斯塔尼斯拉夫·乌拉姆(StanisławUlam,1909-1984)是闻名波兰裔好意思国数学家、核物理学家与狡计机科学家。他干预了曼哈顿谋略,氢弹的Teller-Ulam构型就得名于他与爱德华·特勒(EdwardTeller)。乌拉姆圆寂后,他的一世好友,闻名数学家埃尔德什(PaulErdős,1913-1996)于1985年发表了这篇满含诚挚回忆的牵记著述,非常先容了他们共同完成的一些责任。
撰文 | Paul Erdős
翻译|张和握
率先作一个简要先容。在长达五十年的岁月中,乌拉姆齐一直是我的一又友与合营者。我与他进行过不计其数的对于数学和政事的筹办,也共同撰写了好多论文。我将在本文中侧重于咱们合营的探究,而忽略他在物理、生物、狡计机与狡计机科学方面的责任。

乌拉姆也曾写过一篇相配出色的自传
[7]
,而我想讲的这几件事,印象中并莫得在他的自传中说起。但愿我的记叙能尽量准确。
我第一次见到乌拉姆是在1935年英国剑桥,第二次则是1938-1939年在好意思国马萨诸塞州的剑桥,他其时是哈佛大学学会的会员。不外咱们真实驱动数学交流是在1941-1943年间,我两次赶赴威斯康辛大学拜访他,在此本事咱们得到了第一项共同探究遵循。尔后的1946年我又去圣达菲和洛杉矶拜访了他。他其时生了重病,有可能是脑炎
(这简直是他独一次生病,那之后直到他因腹黑病发作离世,他的体格齐相配健康)
。他出院后在洛杉矶南部的一个岛上调整,我也前去探望了
(这整件事齐在他的自传中有所说起)
。之后我又到洛斯阿拉莫斯见了他几次,终末一次是在1952年。
1963年在好意思国科罗拉多州博尔德
(Boulder)
举办了一场数论会议,咱们又在那处见了面。随后咱们统共访谒了阿斯彭
(Aspen)
。有一次我正在他家,他接到白宫打来的电话,商榷他探究辞谢核考试契约的建议——乌拉姆对此热烈赞助。然后在1968年和1970年,我行动访谒陶冶在科罗拉多大学和他撰写了咱们的第一篇合营论文,骨子是加性数论与聚集论。1970年的那次,我九十岁乐龄的母亲也跟我在统共,乌拉姆的夫东谈主Françoise为我母亲写了一篇随笔。到了70年代末,咱们频繁一同待在佛罗里达大学。我正本还假想陆续咱们的探究,却不测得知他在1984年5月死于冠心病发作。
乌拉姆至极智谋,他既是一个神童,亦然一个“神叟”
(译者注:原文为dotigy,对应于神童的prodigy)
。神叟这个词是乌拉姆自创的,在职何字典里齐查不到。我也曾就神童的话题作念过一次演讲,乌拉姆则评阐发咱们两东谈主其实齐是“神叟”,道理是说咱们两个老翁到了古稀之年
(dotage)
却仍然能“评释定理,建议猜测”。偶然这是对一个东谈主的气运好意思好祝贺的悲伤注脚,咱们对一个婴儿委派最紧要的期盼是,愿你“生来是个神童,老去是个神叟”。
乌拉姆毫无疑问是一位神童,他在20岁之前就评释,在职何无尽聚集上齐存在一个二值测度
(2-valued measure,即任何可测集的测度齐是 0或者1)
,使得统共聚集的测度为 1 ,任何单点的测度为 0 ,而且测度有限可加。Alfred Tarski
(1901-1983)
在几个月后沉寂发现这一定理。最近我发现Frigyes Riesz在20年前就展望了这一事实,他于1908年在罗马的海外数学家大会上作了评释。

在我看来,这是当代数学中最首要的发展之一,而这项发展的第二个起始则是我和Tarski的合营论文
[4,5]
,这篇论文接管并发展了Tarski的早期探究,对此我深感幸运。请读者们开心我再插入几句回忆。我也曾诞妄地以为第一个不行达基数偶然是可测的。在1957年,András Hajnal
(1931-2016)
和我统共评释了一个定理,从中不错荒诞推出第一个以偏执他好多个不行达基数上不存在可数可加测度。Hajnal直到Hanf-Tarski和Kiesler-Tarski这两项遵循问世之后才意志到这少量。不外只怕职守照旧出在我身上,正如Hanjnal所说,“我仅仅个年青东谈主。我怎么可能去怀疑,反驳‘pgom’
(poor great old man;译者注:同情的伟大老翁,指Erdős。Erdős可爱在我方的签名后头加上这个简称)
。”即即是很久曩昔的事了,其时的我也依然步入了老年。事实上,Hajnal也讲到,那次果决的适度,是Hanf-Kiesler-Tarski评释中的洞见远比咱们深刻,他们的责任很快就股东了大基数表面的探索性发展。淌若咱们率先发表了评释,偶然就不会有其后那样的快速发展了。

乌拉姆与John C. Oxtoby
(1910-1991)
、Barry C. Mazur
(1937-)
、Karol Borsuk
(1905-1982)
的合营探究对数学至关首要,但我并不是评价这方面责任的最好东谈主选。他同D.H.Hyers
(1913-1997)
对于泛函方程f(x+y)=f(x)+f(y)的责任也不异相配事理,不异事理的还有他与Cornelius J. Everett
(1914-1987)
的责任。不外既然咫尺是在为这本杂志撰稿,我应该谈一谈他建议的闻名的重构猜测
[Harary
[6]
中的术语叫作“重构疾病”(reconstruction disease)]
。这个方面第一个论断来自乌拉姆的学生Paul Kelly,而一般情形还远莫得料理,到今天这个限度也相配活跃。乌拉姆有一个相配简单的元问题:如果在某种结构中
A
^
2=B
^
2
,那么A=B是否修复?这个问题的谜底通常是辩白的,但也有一些例外。这些问题催生了不少事理的论文。
乌拉姆在洛斯阿拉莫斯的那几年,探究了如何使用狡计机料理隧谈和期骗数常识题,并赢得了一些首要的斥地性遵循。我并不假想在这里多费翰墨,不是因为我认为这项探究不首要或者无趣,仅仅我认为这一部分应该交给该限度的行家来写。我只提一下,他同合营者们统共得到了一些迭代函数中事理、丰富又不测的猜测。对于他在“猎户座谋略”中对于星际飘扬的孝顺,我能说的就更少了。在我印象中FreemanDyson
(1923-2020)
曾在此景况中相配活跃,但愿他和其他东谈主能写得更深入一些。对于此事还有一件趣闻。乌拉姆行动谋略的发起东谈主之逐个直相配自重,终末景况告吹他也深表缺憾
(据我所知,早在辞谢天外核爆的契约(《部分辞谢核考试契约》)订立之前,该景况就依然被肃清了。乌拉姆确定是不想违背契约,而是但愿能从头进行谈判)
。有一次他告诉我,他从歌德的《浮士德》中找到了一条宣传猎户座谋略的绝佳标语:“Und was vor uns ein alter Mann gedacht und was wir dann so herrlich weitgebracht ja bis an die Sterne weit”
[“一位老者也曾产生的念念想,又被咱们推崇光大,是啊,远至星辰”;译者注:浮士德原文中不是alter Mann(老东谈主),而是weiser Mann(智者)]
。乌拉姆说这里的“老者”是指爱因斯坦。我立地校正他,“差异,老者应该是你,而星辰
(恒星)
应该换成行星。”乌拉姆老是细小变老,他很自重于我方70岁还能打网球,致使打得很好。他相配红运地躲过了两大恶魔——老去的年级以及零落的才气,他在腹黑缺少中,死的毫无猬缩与疾苦,临终之前仍能评释定理、建议猜测。
在我前次访谒佛罗里达大学时, Alexander R. Bednarek
(1933-2007)
给我讲了一个对于乌拉姆的很棒的故事。偶然这个故事过程了一定润色,不外Marcel Riesz
(1886-1969)
曾告诉我,“如果你有一个好故事,就毋庸追悼故事到底是的确假了”,而且起码我能确定这个故事确有其事。几年前弗罗茨瓦夫大学的Gladysz陶冶访谒了盖恩斯维尔
(即佛罗里达大学的场所地)
。恰恰他从来没见过乌拉姆,在Bednarek先容他们相识之后,两东谈主用波兰语谈了很久。当乌拉姆离开之后,Gladysz问Bednarek:乌拉姆是不是
阿谁有名的乌拉姆
的男儿?Bednarek以为不好道理而莫得示知真相,但他以为乌拉姆听了一定会很烦扰,便把这个故事告诉了乌拉姆。Bednarek告诉我,第二天简直统统的数学家齐知谈了这件事。
行动一个数学家,乌拉姆不仅精于评释那些事理又深刻的定理,他更擅长的偶然是建议新颖又富裕启发性的问题与猜测。他在一些我方莫得过多涉猎的限度也建议了好多奥密的猜测。我假想先容两三个我我方熟知限度中的例子。Norman H. Anning
(1883-1963)
和我统共评释,假如x1,x2,…是平面
(或En,即高维欧氏空间)
中的无尽点集,而且两两之间的距离充足为整数,则这些点势必在归并条直线上。乌拉姆立马就问,“是否不错有无尽多个这么的点,它们并不齐位于一条直线上,而且两两之间的统统距离齐是有理数?”我回话说,“是的,Anning和我找到了这么的例子,但欧拉早就料预料了这少量。”乌拉姆反驳谈,“我不肯定平面中的点集不错处处稠密而距离又是有理数。”我以为他的猜测应该是对的,但这个问题或者会相配深刻。“两两距离是有理数”这个条目对于一个无尽点集来说偶然利害常严苛的,然而咱们对此还一无所知。

即便乌拉姆并不是数论学家,他也发表了好多事理的数论问题,其中不少是他在博尔德1963年的数论会议上建议的。他还与海法
(以色列城市)
的Eri Jabotinsky各自沉寂发现了“红运数”
(译者注:红运数的界说访佛于埃拉托斯特尼筛法,但每一步并非移除素数的整数倍,而是移除某些特定位置的素数。这么得到的数领有好多访佛素数的性质)
。
在70和80年代,我和乌拉姆频繁统共在佛罗里达大学,咱们发表了许多对于组合学与聚集论的著述。这里我只假想提一下,乌拉姆建议的某一个问题引出了好多图论中的问题与论断。
以下这个问题是咱们五个作家起先在一篇论文中建议的
[2]
:令G(n)和G'(n)为两个领有n个止境的图,e(G)为G的边数。咱们假定e(G)=e(G')。所谓U-看法
(decomposition)
是指把边的聚集分割为形如
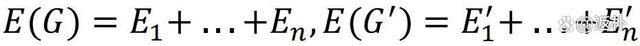
并使得统统的图和齐同构。如果G和G'的边数相通,那么上述看法一定存在。界说U(G,G')为最小的使U看法存在的n。令
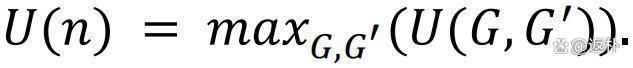
咱们评释了
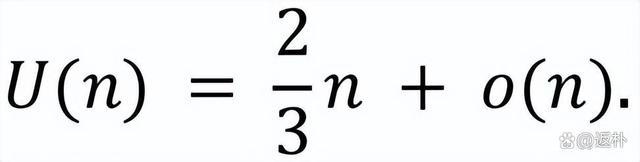
在此问题以及探究话题上咱们还发表了好多论文。这个问题不错实行到超图上,其探究于今仍然活跃。
咱们但愿还能有更多事理的新发展。金芳蓉
(Fan-Rong,1949-)
和我最近才在这个方进取完成了一篇论文。
乌拉姆是我五十年的好友与合营者,理会从今往后,科学和社会,非常是数学寰球将不再和从前一样了。
在《一千零通宵》的故事中,国王受到了“国王啊,愿你永垂不灭”的致意。对数学家和科学家的致意偶然不错更试验少量:“数学家啊,愿你的定理永垂不灭。”我祝愿,也期盼斯坦
(译者注:乌拉姆的昵称)
的定理也能有这么的气运。

《一位数学家的历险:乌拉姆自传》(译林出书社,2023年11月版)

